klioncache.blogg.se - Example of supplementary angle

We know that Sum of Complementary angles = 90 degrees.īy adding 40 degrees to 50 degrees, the total angle becomes 90 degrees.Ģ. The given angle is 50 degrees, then, the Complement is 40 degrees.

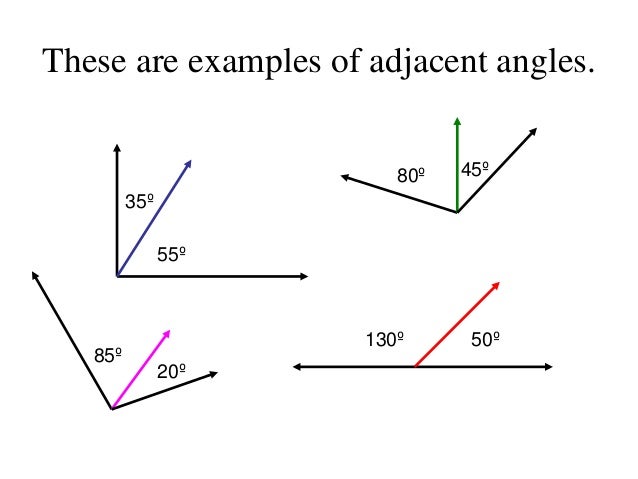
Solved Examples on Supplementary and Complementary Angles In Supplementary Angles, both angles are said to be a supplement to each other. By adding 130 and 50 degrees, it forms a straight line. If x is one angle then (180 – x)° is the other angle in Supplementary Angles.įor example, if 130° is one angle in Supplementary Angles, then the other angle will be 50°. Two angles are added and formed a straight line in Supplementary Angles. The two angles are said to be Supplementary angles if their sum is 180°. Also, two obtuse angles cannot complement each other.Two right angles cannot complement each other.Two complementary angles are acute but vice versa is not possible.70° and 20° complement each other.Įxample 1: To find the complement of 3y + 52°, subtract the given angle from 90 degrees.ĩ0º – (3y + 52º) = 90º – 3y – 52º = -3y + 38º If x° is one angle then (90 – x)° is the other angle in Complementary Angles.įor example, if 70° is one angle in Complementary Angles, then the other angle will be 20°. Each angle is called the complement of the other. The two angles are said to be complementary angles if their sum is one right angle i.e. Also, we have given all the concepts available in Lines and Angles on our website. Find different problems on Supplementary and Complementary Angles in this article. Or else, if the sum of the two angles is 180º, they are called Supplementary angles. If the sum of the two angles is 90º, they are called Complementary angles. In Euclidean geometry, any sum of two angles in a triangle is supplementary to the third, because the sum of internal angles of a triangle is a straight angle.Complementary and Supplementary Angles are the angles formed by adding two angles. Their cosines and tangents (unless undefined) are equal in magnitude but have opposite signs.

The sines of supplementary angles are equal. If a point P is exterior to a circle with center O, and if the tangent lines from P touch the circle at points T and Q, then ∠TPQ and ∠TOQ are supplementary. For example, adjacent angles of a parallelogram are supplementary, and opposite angles of a cyclic quadrilateral (one whose vertices all fall on a single circle) are supplementary. However, supplementary angles do not have to be on the same line, and can be separated in space. Such angles are called a linear pair of angles. have a common vertex and share just one side), their non-shared sides form a straight line. If the two supplementary angles are adjacent (i.e.

Two angles that sum to a straight angle ( 1 / 2 turn, 180°, or π radians) are called supplementary angles.

The angles a and b are supplementary angles. For example, the angle with vertex A formed by the rays AB and AC (that is, the lines from point A to points B and C) is denoted ∠BAC or B A C ^ (The tangent of an angle equals the cotangent of its complement and its secant equals the cosecant of its complement.) The prefix " co-" in the names of some trigonometric ratios refers to the word "complementary". In geometric figures, angles may also be identified by the three points that define them. See the figures in this article for examples. In contexts where this is not confusing, an angle may be denoted by the upper case Roman letter denoting its vertex. Lower case Roman letters ( a, b, c, . . . ) are also used.

In mathematical expressions, it is common to use Greek letters ( α, β, γ, θ, φ, . . . ) as variables denoting the size of some angle (to avoid confusion with its other meaning, the symbol π is typically not used for this purpose). The first concept was used by Eudemus, who regarded an angle as a deviation from a straight line the second by Carpus of Antioch, who regarded it as the interval or space between the intersecting lines Euclid adopted the third concept. According to Proclus, an angle must be either a quality or a quantity, or a relationship. Įuclid defines a plane angle as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other. Both are connected with the Proto-Indo-European root *ank-, meaning "to bend" or "bow". The word angle comes from the Latin word angulus, meaning "corner" cognate words are the Greek ἀγκύλος (ankylοs), meaning "crooked, curved," and the English word " ankle". 4.4 Alternative ways of measuring an angle.